A Planetarium for Every Classroom
Building and Using a Planetarium for Your Classroom Using Inexpensive Materials

2-frequency 2-meter dome

For individual or small groups of students

We move next into building a larger scale, more spherical dome. The plans presented here are for a dome with a radius of 1 m, so the finished dome is 2 meters across.

A dome with a radius of 1 meter will be about 6 feet across when assembled, and will be useful for large-scale demonstrations or small model planetariums. It is not large enough to have more than a few students sit inside when completed (unless your students are very young!)

Materials needed:

Background
This dome is a 2v, or two-frequency dome. Plans are not presented here to make this into a sphere, although you could easily do so by adding additional triangles and continuing the pattern. Two different triangle sizes are used.

You will need to use stronger materials than paper or construction paper. Posterboard might be strong enough if the dome is carefully assembled. Fibreboard, such as is used for science fair displays, is suitable. The best kind of cardboard is corrugated cardboard because of its strength. Cutting corrugated cardboard isn’t easy and scissors are probably not the best tool to use. In some cases, if you use box cutters to cut one side of the cardboard following a straightedge, you can fold the cardboard along the cut and just snap it apart. Otherwise, turn the cardboard over and fold it into a V-shape, then cut in the narrow channel that results.

If fiberboard is used and it has only one white side, be sure to make the white side the interior of the dome so it doesn’t need to be painted. If you have access to a paper manufacturing facility, sometimes cardboard can be purchased with one side already made white for producing white cardboard boxes. Such cardboard typically comes in 4 x 8 foot sheets, and you should take care not to bend it until absolutely necessary in order to retain its strength. It is entirely possible to build the dome out of scrap cardboard from a variety of boxes, and a grocer or warehouse store probably has lots of boxes they would be willing to donate to your project.

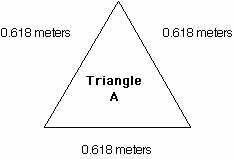
If you don’t have white cardboard, you should paint one side of the cardboard white with any white flat paint. See painting tips for other hints, but for now it is best to note that painting is probably best done before the cardboard is assembled into a dome. The connecting flaps do not need to be painted.

Procedure:
This dome uses two different size triangles. To create a dome with a radius of one meter, construct the following templates for use in tracing triangles on other pieces of cardboard.

1. The first triangle is an equilateral triangle with each side equal to 0.618 meters, or 61.8 centimeters. Do not leave any extra cardboard for connecting flaps. This will be called triangle A. Make one of these.

2. The second triangle template is an iscosceles triangle, which means two sides are the same length and the third side is different. In this case, the two identical sides are 0.546 meters long, and the third side is 0.618 meters long (the same as triangle A.) This is called triangle B. Make one of these.

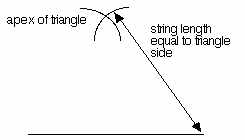
One way to make the template accurately for these triangles is to use an old geometry technique. First, draw the base the triangle with a pencil and ruler. Next, measure a length of string equal to one of the remaining sides, and draw an arc centered on one end of the line you drew. Repeat on the other side, and where the arcs cross must be where the top of the triangle is located.

3. Once you have the templates made, assemble enough cardboard to make the remaining triangles. You will need to make 10 A-type triangles and 30 B-type triangles.
Each time you make a triangle, trace the shape from the template so that all the triangles are identical. This will work better than measuring from scratch each time. You need to leave about a 5-cm (2 inch) flap along each edge to use when connecting the triangles together. A single completed triangle will look like this.

The connecting flaps for this dome will need to be folded carefully so they bend straight. In this case score the cardboard by drawing a heavy line with a ball-point pen (not a felt-tip) which will weaken the bending joint. Then bend the cardboard along the line you drew to make a flap or other junction. Don’t be afraid to practice on some scrap before committing yourself to a more permanent part.
Another good idea is to label the outside of the triangle with the type, A or B; when you have a stack of triangles it can be difficult to tell which is which. The outside of the triangle is the side the flaps bend toward.

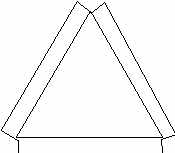
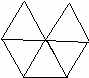
4. At this point you must decide and commit to using a particular method of attaching the flaps together. You need to decide if you want to use nuts and bolts or binder clips.
Nuts and bolts are better for permanent assembly, especially if you plan to use the dome several times before disassembling it. Their primary advantage is strength and permanence. They have the disadvantages of being slower to assembleIf you are using bolts and washers, separate the parts into small bins for easy assembly, and have extras just in case. You will need approximately 4 bolts, 4 nuts, and 8 washers for each joint in the design. A total of 75 sets of 4, or 300 bolts, 300 nuts, and 600 washers will be sufficient for all junctions plus having ome spares. You should get the largest washer which can be held by the bolt, as small washers might pull through the cardboard if the dome experiences much stresss. A 3/4 inch long bolt should be sufficient for the assembly.
The other workable alternative is binder clips, the large black triangular kind you get from office supply stores. Three or four per joint should be sufficient, and so 225 to 300 clips will be required. One student who built a larger dome with clips proclaimed, “You can never have too many clips,” so consider buying extra for loss and breakage and reinforcing weak spots. The advantages of clips are ease and speed of construction. Their primary disadvantage is they do not take a lot of force to pop loose and slip. This is your best choice if you wish to assemble a temporary dome. When disasembled, the parts fit nicely in a large box or behind a cabinet.

5. To assemble the dome using your chosen method of assembly, begin by building a pentagon of 5 B triangles, with the long sides all on the outside

.

Leave the last joint unconnected until last to make the assembly easier.Connect the last two interior sides together to make a little “cap” or bowl shape.

6 . Make 5 more of these pentagon shapes.Set one of the pentagons aside.

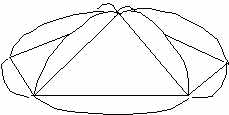
7. Set 5 pentagons into a circular pattern on the floor, stand two at a time up on one edge, and insert an “A” triangle between them. If you are working alone, having lots of chairs around to brace things is helpful.
View of 5 pentagons separated by “A” triangles, seen from above. “A” triangles are black in this illustration.

8. Insert another “A” triangle into the gaps at the tops of the pentagons, this time with the point of the “A” pointing downward.

Finally, set the remaining “B” triangle pentagon into the remaining hole and attach with clips. Again, two people working at once is much easier, especially on the larger domes

.

Congratulations! You have assembled your 2-frequency geodesic dome!

Here is a photo of an assembled 2 meter dome with flaps inward.

Click here for a printable version

Site counter courtesy of www.digits.com

This project was supported by a County Technology Academy Grant funded by the Dean and Margaret Lesher Foundation in cooperation with the Contra Costa County Office of Education.